Discontinuous functions and C++0x
On the Graphing Calculator Users List, David Craig pointed out an interesting bug.
"A formula for a conic section in polar coordinates is r=A/(1+Ecos&theta) where A and E are constants. E is the eccentricity. When E is increased past one so that the section is hyperbolic, GC 'crosses' the hyperbola. This is distracting."
![]()
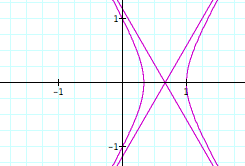
The bug occurs because GC samples the function at discrete points and connects them with line segments. Where the denominator goes to zero, the function is not continuous, but GC does not notice and blithely connects points sampled on separate branches of the hyperbola.
To do this correctly, GC should check that the function is defined and continuous everywhere on the interval between the sampled points. One of the proposals to the C++ standard committee meeting last month in Portland, N2137: A Proposal to add Interval Arithmetic to the C++ Standard Library provides just such a mechanism for checking continuity, by using interval arithmetic and passing an additional flag with each calculation to check if the function is defined and continous everywhere on an interval.
Jeff Tupper's GrafEq software, for example, uses interval arithmetic and continuity-tracking to rigorously prove the existence of a solution to the given equations in any pixel it draws. The image below is from GrafEq:
For now, the simplest way to work around the problem in GC is to explicitly tell it in the equation to ignore points too close to where the denominator is zero, by graphing the following instead: