The Library of Babel function
![]()
MathWorld calls this Tupper's Self-Referential Formula because a graph of that inequality in the domain 0<x<105, N<y<N+16 for a particular 541-digit number N shows an image of the function itself.
Closer investigation reveals that MathWorld does not even begin to do justice to the function, for higher up on the graph of this function one can find the complete works of Shakespeare, the contents of the lost library of Alexandria, and perhaps even the solution to unifying quantum mechanic with general relativity! At y values nearer the origin, you can find tomorrow's winning lottery number! If that sounds unbelievable, read on....
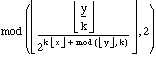
Consider rearranging the function slightly, as above, with k=17. Then note that in the domain used, N<y<N+k-1 the numerator, floor(y/k) is a constant. Let's call that constant B. As a computer graphics programmer, the structure of the denominator of that fraction jumps out to me eye. The image appears in a rectangle 105 pixels wide by 17 pixels tall. Let's call the integer parts of x and y, ix=floor(x) and iy=floor(y). The term mod(iy,k) counts from 0 to 16. The exponent k*ix + mod(iy,k) just counts from 0 to 105*17-1, sequentially, moving first up each column, and starting over at the bottom of the next column. So let's label index=k*ix + mod(iy,k) as an index pointing to the pixel at (ix, iy). As an old C programmer, I see division by 2^index and recognize that as a bit-shift, moving the bits in B to the right by index. Taking mod 2 of an integer just asks if it is even or odd, or thinking of it another way, asks the value of the least significant bit in the binary representation of that number. Performing a bit-shift to the right, and then taking that value mod 2, is a way of asking
What is the value of the bit at position index in the binary representation of B?
The graph of the formula contains every possible black and white bitmap of height k, in order, as you move up along the y-axis from the origin!
The particular 541 digit number chosen is, essentially, the integer representation of the bitmap. To see this directly, you can graph this function using the Unix utility bc by issuing the following commands in Terminal on Mac OS X, for example:
setenv BC_LINE_LENGTH 19
This tells bc to format its output with 17 characters to the line (not counting the \ and return character at the end of each line.)
bc
obase=2
That tells bc to display output results in binary, base 2.
print"\n",0,0,(960939379918958884971672962127852754715004339660129306651505519271702802395266424689642842174350718121267153782770623355993237280874144307891325963941337723487857735749823926629715517173716995165232890538221612403238855866184013235585136048828693337902491454229288667081096184496091705183454067827731551705405381627380967602565625016981482083418783163849115590225610003652351370343874461848378737238198224849863465033159410054974700593138339226497249461751545728366702369745461014655997933798537483143786841806593422227898388722980000748404719/17)
To get the 105 x 17 pixel rectangle to line up, the line above tells bc to print two leading zeros. If you then turn your head sideways and squint, or copy the output to a text editor and replace 0 with space and 1 with * to squint slightly less, you can see the bitmap image of the function.
This Graphing Calculator document graphs the case for k=1 enumerating all 1-pixel high bitmaps as you travel up the y-axis, which is just like counting in binary.

This Graphing Calculator document constructs the magic number B to find the first image of a "+" sign along the y-axis for the case k=3.
Number the pixels in a 3x3 bitmap like this: 2 5 8 1 4 7 0 3 6 Draw a "+'" sign in a 3x3 grid like this: .*. *** .*.
![]()
Then look at 558<y<561 since 3*(2+8+16+32+128)=558.
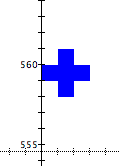
Comments
I once thought of building an array of LEDs that counted in binary so that it would display the complete works of humans previous and future. But after calculating how long it would take even at an unrealistic clock frequency with a decent number of pixels, I gave up since the earth would be destroyed by the sun sooner than my box having finished it's task. The problem, as I see it, with these endeavors is not the output of the content, but rather the identification of garbage, repeated versions of previous outputs (such as Shakespeare in Helvetica type or in Geneva), and meaningful entries. I then concluded that a true intelligence is something of a search algorithm.
And to your exploration of this topic, I commend you for seeing through deceptive significance of a construct.
I looked at Wikipedia's entry for "illegal primes" similarly on my blog. With file meta data, comments with code, and use of birthday attack techniques, one could generate a prime number to represent any data. But there are just as many if not more primes that are nonsensical if treated the same way.
Posted by: Mike | January 28, 2007 10:42 AM