Dependencies
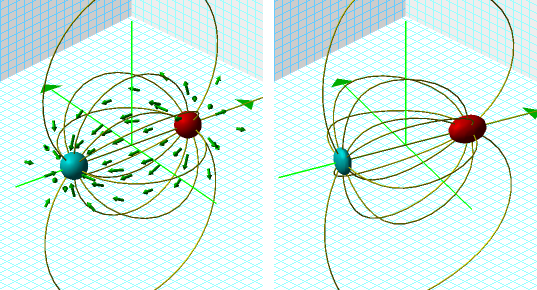
Consider a dipole field as a gravity wave passes distorting space. On the left are positive and negative charges drawn as spheres, a vector field drawn as arrows, and field lines drawn as tubes. The right shows the objects under a coordinate transformation of a compression wave travelling along the x-axis.
Here is an animated movie.
Now, consider each equation.
First, each is constructed as a separate object which can is evaluated in parallel threads. However, the transformed equations refer to the solutions of the untransformed equations, so they can't begin calculating until the first are done. The spheres are given as implicit equations which as solved by evaluating the function on a cubic lattice then root-finding along the edge of each cube. This is computationally expensive, but also embarrassingly parallelizable and subdivided into as many tasks as the computer has CPU cores. Each field lines is computed by an ODE solver. The ODE intial conditions are specified here as points distributed about a surface described by an implicit equation. As that implicit equation is solved (which itself could be done in parallel), each field line is an independent calculation submitted for threaded parallel execution. The transformed tubes and surfaces on the right are also done in parallel. The details, as with all programming, are ensuring that each calculation does not begin until the results it is dependent upon are complete, and ensuring that calculations running in parallel are truly independent of one other.
I spent last week parallelizing the code which implements this, reviewing it for race conditions arising from dependencies between components. While conceptually straightforward, the actual programming required delicate care.
How many race conditions do I see? Let me count them, one, tthwreoe.
Comments
Now what are the chances that I'd pick up two articles mentioning gravity waves in the same hourly batch of RSS feeds (neither of them particularly physics-centric)?
http://commentisfree.guardian.co.uk/daniel_davies/2006/10/faking_the_physics.html
Posted by: Jonathan Lundell | October 14, 2006 09:44 PM
Chad Orzel discusses the 'Harry Collins' thing here.
My example actually has nothing to do with gravity waves. Aside from being 'not drawn to scale' by about thirty orders of magnitude, the transformation equations are all wrong. The only point of contact is the notion of deforming the underlying space.
Posted by: Ron | October 14, 2006 09:58 PM